最值在中考数学中属于高频考点，不管几何照旧二次函数压轴题，都有它的影子。

但二次函数和几何中求最值平庸是不相同的：

几何题中经常需要转变成几何问题，隐圆、旋转、对称……比拟难想；

而二次函数中陆续用解析法，哪怕是作念援助线，也比拟容易猜度，难点在谋略上。

我们来看底下的例题。

01

解析法

解析法，简便一些来说，就是：

把问题用代数，方程或者函数抒发出来，再通过函数或代数式的性质，来不休相应问题。

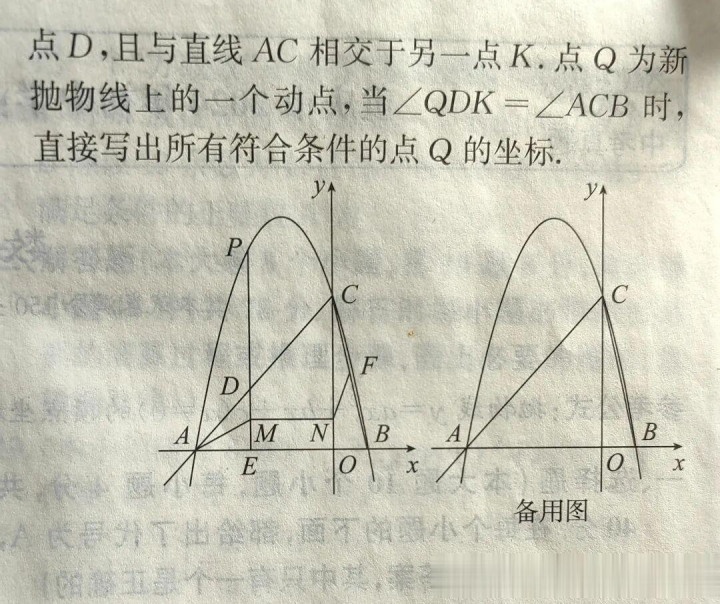
在初中高中这里，具体的就是：

把几何、物理问题跟函数皆集起来；

再放到坐标系内；

利用坐标系来琢磨函数的性质，从而不休几何和物理问题。

我们常作念的二次函数压轴题就是这个类型。

高中的圆锥弧线，还有立体几何中的缔造坐标系，亦然用解析法不休问题。

当今中考、高考又出了许多新题型，亦然函数和推行问题皆集，放到坐标系中——

谋略是让学生学会用解析法不休问题。

这些记好，如斯便明确出题谋略，学习主义，题目中的数学想维。

底下我们看题谋略第一问。

第一问很简便，大部分同学都会作念，这亦然一个通例操作。

这个通例操作就两分，然则通过它我们要光显：

在坐标系内，点妥协析式的对应干系。

这个干系，是后续谋略的基础——就比如第二问，求一个最值。

要求最值，你需要三步：

第一双应，点在抛物线上，怎样用解析法抒发点的坐标；

第二运算，默示出来坐标，让坐标点参与运算，进行代数推理；

第三想考，利用一些几何学问，皆集代数式不休问题。

先看第一步。

点在抛物线上、点在直线上，笔据这些条款要会设点的坐标。

这里暗含一层预想，点在抛物线（直线）上，就是这个点得志抛物线（直线）的解析式。

既然得志解析式，解析式实质上亦然一种函数；

我们就可以利用函数的性质来分析点，来作念运算，来不休问题。

接下来第二步，让点的抒发式参与运算。

PD获得最大值——奈那处理？

PD之间的距离，是可以用坐标系内的点的坐标来默示的。

比如小学生都会学：

你在（2，2）这个位置，我在（2，1）——我们在并吞列不同的行。

我们之间差一个单元的距离，谋略起来就是2-1=1。

那么PD的长，我们就用P的纵坐标减去D的纵坐标，得出一个距离的抒发式——

小学生不可这样搞，代数想维是很详细的，他们的详细才气还莫得达到这个级别。

在详细坐标系内的运算，他们只可剖释具体的数。

而初中生可以剖释代数详细了，这里再讲一遍是我们要把意见的根柢逻辑搞明晰。

接着看：

距离的抒发式亦然一个函数，我们可以利用函数的性质来类比不休最值问题。

对应到这里就是一个二次函数，二次函数有最值、有最值点；

找到它的最值和最值点PD距离的最大值就不休了——这就是解析。

第三，更复杂的，求AM+MN+NF的最小值，需要少量想考。

我们要利用少量几何学问了。

因为MN定值，那么AM+MN+NF的长度，就取决于AM+NF了。

我们都知谈：两点之间线段最短，那么唯有ANF在一条线上，就OK了。

都不挨着，奈何办？

平移，平移是我们平庸用的妙技。

这就是几何要领——在几何压轴题里也常用，届时笔据时事需要我们也会作念平移。

如下图，平移之后A'N'F就在一条线上，这样就转变成求一条线段的长度了。

坐标系内求线段长度，有“两点之间的距离公式”，或者，也可以用勾股定理。

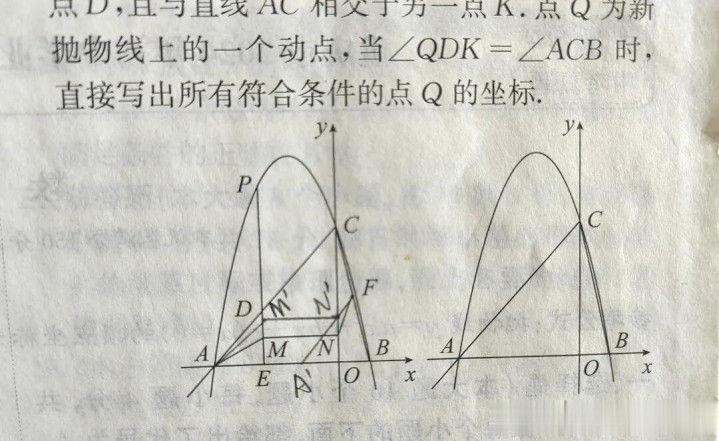
勾股定理适值合适了坐标系内运算的端正。

我们说坐标系内的点，不管它的横坐标照旧纵坐标，都是跟坐标轴垂直主义的对应点。

即就是x轴，亦然垂直于y轴的。

那么这样的垂直，就很容易组成直角三角形；

既然是直角三角形就很容易利用勾股定理。

这亦然坐标轴内解析法的妙处——可以把许多学问点都迁徙到坐标轴里来。

我们再往下看第三问，先画绘图。

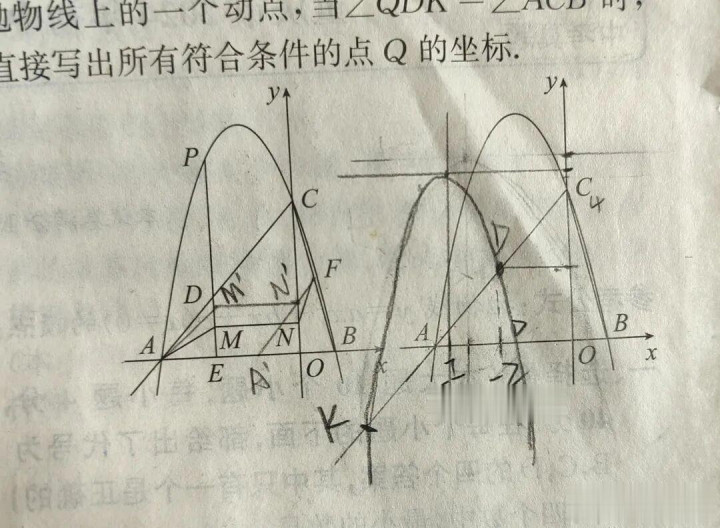
为什么或者画出这张图呢？因为我知谈沿着直线平移怎样平移。

简便来说就是：看主义，依旧是左加右减，上加下减。

沿着CA，是向左，向下；

那么平移后解析式抒发出来；

再笔据经过的点来求平移的单元。

——坐标系里，函数的一些端正，我们也要知谈少量。

不单是是把几何问题迁徙到坐标系内，坐标系内的一些规矩，我们也要光显一些。

等于一个地界有一个地界的规矩，这些个规矩，我们得懂。

这要看浅薄的学习积聚了——作念学问，偷不得懒哦。

既然有新的解析式和图像，我们就可以算出它与直线的交点k。

这照旧要笔据对应来。

有交点，交点在直线上也在抛物线上，那就是它们的纵坐标异常；

我们便可以联立方程，或者径直让他们的解析式异常。

这亦然求交点的习用操作——包括以后的圆跟直线交点，椭圆跟直线交点……

解析系统里有许多操作，都是前东谈主归来，这些操作你最佳都网罗一下！

利用这些操作，熟习使用这些操作，会匡助你快速通向谜底。

接着来，当我们联立方程，便能求出k值，接着Q点的位置我们就可以笔据条款揣摸了。

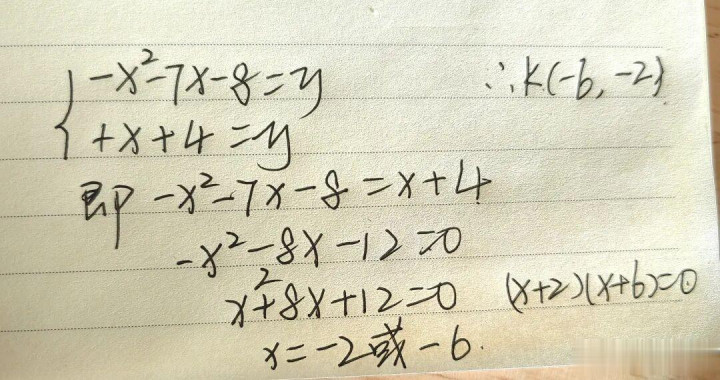
这本事，你需要一些【教会】。

∠QDK=∠ACB，假如k在AC的下方，DK和BC是平行的。

既然平行，那么这两条抛物线还彼此平行，那么我们就可以想见：

K和Q的纵坐标是疏通的;

既然纵坐标疏通，我们就可以精炼算出Q点.

——这就是教会，也可以说是直观。

这种题让径直写出合适条款的点，靠教会和直观就行，省时分。

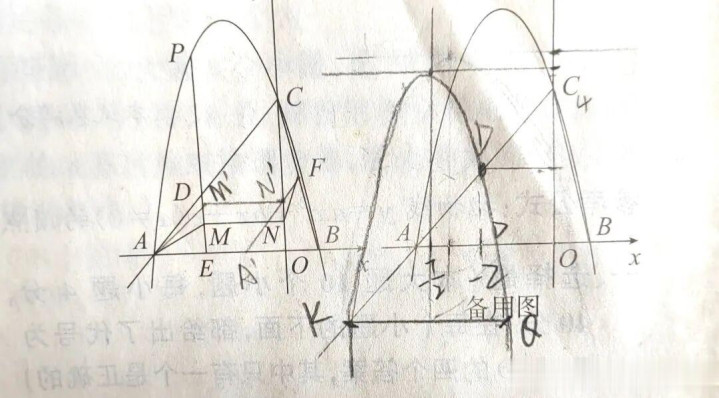
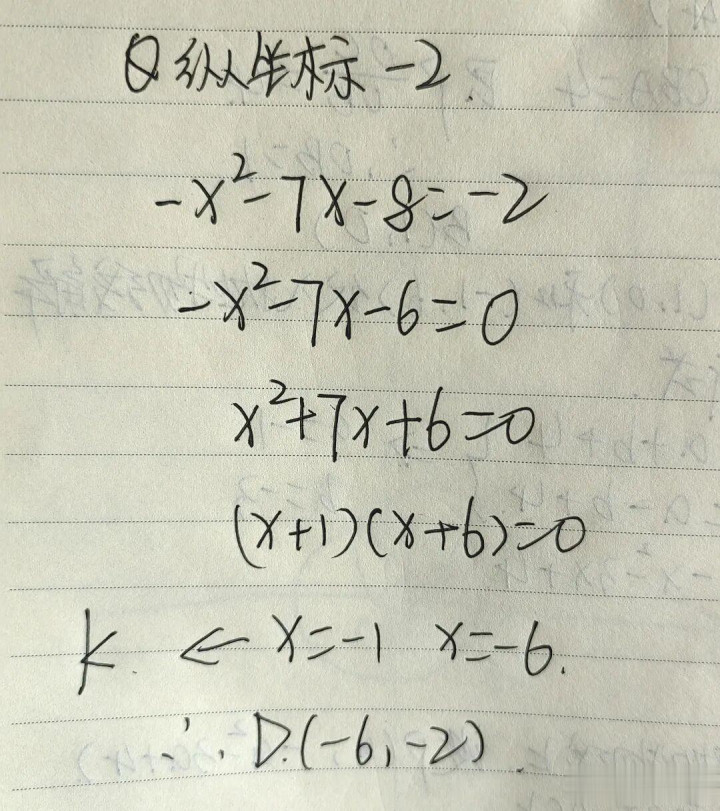
而剩下一个点，靠教会和直观就不行了。

直观上这个点就在AC的上方，但你还不可径直就让它跟Q1对称，不一定的。

我们需要想考——作念出这一问，就靠个东谈主才气了。

分析：

既然Q2在AC的上方，又因为∠QDK=∠ACB，AD=AD,我们可不可以构造一个三角形；

∠DAB=45°，我们只需要另外一个等于45°的角；

于是，我们可以过A作GA⊥X轴，△GAD≌△DAH.

接着我们就可以笔据线段异常来谋略了。

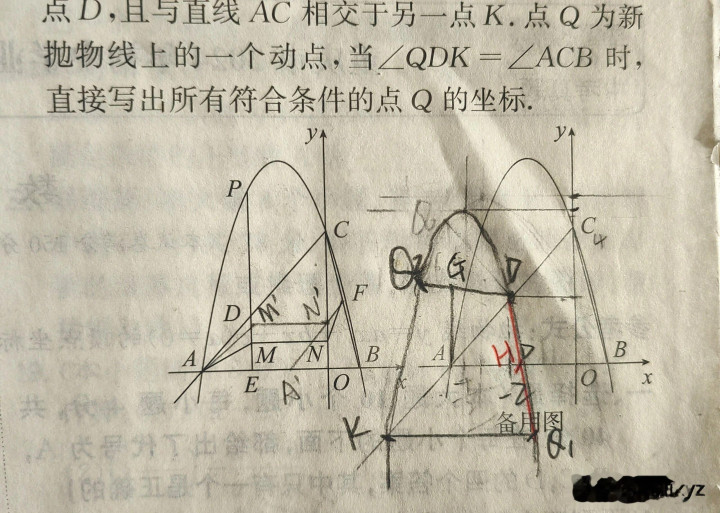
经过谋略我们找到了Q2，找到这个点，果然需要才气。

若是作念不出来，作念到Q1仍是很可以了——谋略历程也很复杂，一不戒备就错了。

好，题目作念完毕。

到这里，你也看出来了，二次函数大题其实就是解析法的终极试真金不怕火。

解析法是一个很好的器用，我们数学老师的谋略就是：陶冶生使用数学器用。

不是统统东谈主都可以发明器用，也不要追求这个——创意使用器用，仍是很了不得了。